Bahan Ajar Kelas 5 - KPK dan FPB - Dewanto Huang

Konten [Tampil]

Selamat datang di layanan blog pembelajaran yang ditulis oleh Mr. Dewanto, S.Pd. (黃亞財). Pada unit pembelajaran ini, kita akan mempelajari terkait KPK dan FPB sebagai materi pembelajaran matematika di Kelas 5. Adapun tujuan pembelajaran yang akan dicapai, yaitu:

Peserta didik dapat menentukan kelipatan (multiple) dan kelipatan persekutuan (common multiple) suatu bilangan.
Peserta didik dapat menentukan faktor (factor) dan faktor persekutuan (common factor) suatu bilangan.
Peserta didik dapat menentukan bilangan prima (prime numbers).
Peserta didik dapat menentukan faktorisasi prima (prime factorization) suatu bilangan.
Peserta didik dapat menentukan KPK (LCM/Least Common Multiple) dan FPB (GCF/Greatest Common Factor) dengan faktorisasi prima (prime factorization).
Peserta didik dapat menyelesaikan masalah yang berkaitan dengan faktor (factor) dan kelipatan (multiple).

Kelipatan (Multiple)

Kelipatan suatu bilangan merupakan bilangan-bilangan yang merupakan hasil kali bilangan tersebut dengan bilangan asli (N = {1, 2, 3, 4, 5, ..., dan seterusnya}). Perhatikan contoh di bawah ini dengan seksama!

Kelipatan 4 = 4, 8, 12, 16, 20, 24, ...., dan seterusnya
Kelipatan 2 = 2, 4, 6, 8, 10, 12, 14, ..., dan seterusnya
Kelipatan 3 = 3, 6, 9, 12, 15, 18, 21, ...., dan seterusnya

Berdasarkan contoh di atas, kita dapat mengetahui bahwa kelipatan merupakan pengulangan dari suatu bilangan. Tentu saja untuk mempermudah kamu dalam mengetahuinya akan lebih mudah jika kamu terampil dalam perkalian bilangan.

Kelipatan Persekutuan (Common Multiple) dan KPK (LCM)

Kelipatan persekutuan merupakan kelipatan-kelipatan yang sama minimal dari dua bilangan atau lebih. Arti persekutuan sederhananya dapat diartikan sebagai persatuan atau perkumpulan. Perhatikan contoh di bawah ini dengan seksama!

Tentukan kelipatan persekutuan dari 3 dan 4! Penyelesaian: (1) tentukan terlebih dahulu masing-masing kelipatan dari 3 dan 4. (2) Cari angka yang sama pada kelipatan 3 dan 4. Angka-angka tersebut disebut sebagai kelipatan persekutuan (common multiple).

Kelipatan 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, ..., dst.
Kelipatan 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ..., dst.
Kelipatan persekutuan 3 dan 4 = 12, 24, 36, ..., dst.
Kelipatan Persekutuan Terkecil (KPK) = 12

Coba kamu perhatikan pada pola kelipatan persekutuan di atas! Kelipatan persekutuan dari 3 dan 4 dapat secara cepat kita identifikasi hanya dengan mengetahui kelipatan pertama (angka yang sama dari kelipatan 3 dan 4) lalu tinggal kamu gandakan saja. Perhatikan pada kelipatan 3 dan 4, persekutuan pertama dapat ditemukan pada angka 12. Selanjutnya, kamu tinggal menggandakan saja angka 12 tersebut. Maka kelipatan persekutuan 3 dan 4 = 12, 24, 36, 48, 60, 72, 84, 96, ...., dst. Kelipatan persekutuan 3 dan 4 dimulai dari 12, 24, 36, 48, 60, 72, 84, 96, ...., dst., kelipatan persekutuan yang paling kecil yaitu angka 12. Maka, 12 dinyatakan sebagai Kelipatan Persekutuan Terkecil (KPK) atau dalam Bahasa Inggris dikenal Least Common Multiple (LCM).

Faktor (Factor)

Faktor suatu bilangan merupakan bilangan-bilangan yang membagi habis suatu bilangan. Perhatikan contoh di bawah ini dengan seksama!

Faktor dari 12 = 1, 2, 3, 4, 6, 12
Berdasarkan dari faktor dari 12 di atas yaitu 1, 2, 3, 4, 6, dan 12. Jadi, angka-angka tersebut dapat habis membagi 12.

Faktor Persekutuan (Common Factor) dan FPB (GCF)

Faktor persekutuan merupakan faktor-faktor yang sama dari dua bilangan atau lebih. Perhatikan contoh di bawah ini dengan seksama!

Tentukan faktor persekutuan dari 12 dan 18! Penyelesaian: (1) tentukan terlebih dahulu masing-masing faktor dari 12 dan 18. (2) Cari angka yang sama pada faktor 12 dan 18. Angka-angka tersebut disebut sebagai faktor persekutuan (common factor). Faktor persekutuan mempunyai faktor dengan nilai terkecil hingga terbesar. Faktor persekutuan yang mempunyai nilai terbesar kita kenal dengan Faktor Persekutuan Terbesar (FPB). atau dalam Bahasa Inggris dikenal Greatest Common Factor (GCF).

Kelipatan 12 = 1, 2, 3, 4, 6, 12
Kelipatan 18 = 1, 2, 3, 6, 9, 18
Faktor persekutuan 12 dan 18 = 1, 2, 3, 6
Faktor Persekutuan Terbesar (FPB) = 6

Bilangan Prima, Faktor Prima, dan Faktorisasi Prima

Untuk dapat memahami pembelajaran yang akan kamu pelajari, kamu perlu mengetahui konsep berikut ini dengan seksama!

Bilangan prima (prime numbers) merupakan bilangan yang hanya mempunyai 2 faktor saja, yaitu 1 dan bilangan itu sendiri. Contoh: 5 merupakan salah satu bilangan prima di mana 5 hanya dapat dibagi oleh 2 faktor saja, yaitu 1 dan 5 itu sendiri. Untuk bilangan prima sendiri dapat kamu liat pada Gambar 1, bagian nomor yang diwarnai biru-keunguan merupakan himpunan dari bilangan prima ( P = {2, 3, 5, 7, 11, 13, 17, 19, 23, ....}.

Gambar 1. Bilangan prima hingga 100 (sumber: DadsWorksheets.com)

Faktor prima (prime factor) merupakan faktor-faktor dari suatu bilangan yang merupakan bilangan prima. Contoh: faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12. Faktor prima dari 12 adalah 2 dan 3.
Faktorisasi prima (prime factorization) merupakan cara menyatakan suatu bilangan dalam bentuk perkalian bilangan-bilangan prima. Cara menentukan faktorisasi prima dapat dilakukan salah satunya menggunakan metode pohon faktor. Perhatikan cara menentukan faktorisasi prima berikut dengan metode pohon faktor pada Gambar 2!

Gambar 2. Metode pohon faktor

Menentukan KPK dan FPB

Kita dapat menentukan KPK dan FPB dengan menggunakan beberapa cara atau teknik. Sebelumnya kita sudah menentukan (1) KPK menggunakan kelipatan dua atau lebih bilangan serta menentukan FPB menggunakan faktor dua atau lebih bilangan. Selanjutnya, (2) KPK dan FPB dapat ditentukan dengan menggunakan metode pohon faktor. Terakhir, uraian materi ini akan mengajak kamu untuk menentukan (3) KPK dan FPB menggunakan metode sengkedan. Perhatikan cara menggunakan metode sengkedan berikut dengan seksama pada Gambar 3!

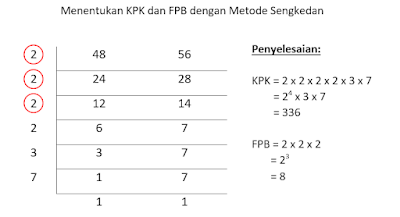Gambar 3. Metode sengkedan

Penjelasan terkait pengggunaan metode sengkedan:

Metode sengkedan dapat digunakan untuk mencari KPK dan FPB sekaligus.
Metode sengkedan membagi bilangan dengan bilangan prima.
Untuk bilangan prima yang dapat membagi kedua atau lebih bilangan, maka bilangan prima itu ditandai dengan lingkaran sebagai penanda.
Untuk bilangan prima yang hanya dapat membagi salah satu bilangan, maka bilangan prima itu tidak perlu ditandai dengan lingkaran sebagai penanda.
Penggunaan metode sengkedan dinyatakan selesai apabila semua bilangan menghasilkan 1.
KPK dengan metode sengkedan merupakan semua bilangan prima dalam bentuk faktorisasi prima. Pada contoh di atas, KPK didapatkan dengan mengalikan semua bilangan prima: 2 x 2 x 2 x 2 x 3 x 7 = 336.
FPB dengan metode sengkedan merupakan semua bilangan prima dalam bentuk faktorisasi prima yang ditandai dengan lingkaran. Pada contoh di atas, FPB didapatkan dengan mengalikan semua bilangan prima yang dilingkari: 2 x 2 x 2 = 8.
Begitulah cara menggunakan metode sengkedan, untuk lebih dari 2 bilangan pengerjaannya sama seperti di atas.

Permasalahan yang Melibatkan KPK dan FPB

Bagian ini akan menampilkan beberapa masalah-masalah dalam kehidupan sehari-hari yang dapat diselesaikan dengan menggunakan konsep KPK maupun FPB. Silakan kamu simak dan pelajari dengan sungguh-sungguh bagian ini ! Bagian ini membutuhkan keterampilan dalam bernalar kritis!

Kasus 1: Aldi, Adi, dan Alya les matematika di tempat yang sama. Namun, mereka mempunyai jadwal les yang berbeda-beda. Aldi les matematika 2 hari sekali, Adi les matematika 3 hari sekali, sedangkan Alya les matematika 4 hari sekali. Jika hari ini tanggal 12 September 2024 mereka les bersama-sama, kapan mereka akan bertemu kembali sehingga dapat les berbarengan lagi? Perhatikan penyelesaiannya pada Gambar 4!

Gambar 4. Penyelesaian kasus 1

Kasus 2: Mr Dewanto mempunyai beberapa hadiah kecil terdiri atas 24 pena, 18 penghapus, dan 16 sticky note yang rencananya akan dibagikan ke beberapa siswa di kelas matematikanya. Jika Mr Dewanto ingin membagi ketiga jenis hadiah kecil tersebut sama rata, berapa siswa yang bisa dibagikan oleh Mr Dewanto? Perhatikan penyelesaiannya pada Gambar 5!

Gambar 5. Penyelesaian kasus 2

Pengayaan (Student Enrichment)

For upgrading your skills in math, especially in Least Common Multiple (LCM) and Greatest Common Factor (GCF), you can try to explore this material below directly by yourself! This materials originally constructed by Khan Academy. [Notes: you are able to access this enrichment when you already understand all materials written by your teacher in this blog article].

Referensi

Fitrianawati, M., Surtiani, I., & Istiandaru, A. (2022). Matematika untuk SD/MI Kelas V. Jakarta Selatan: Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi.
Gunanto & Amalia, D. (2023). ESPS Matematika untuk SD/MI Kelas V. Jakarta: Penerbit Erlangga.
Karso, Suyadi, G., Muhsetyo, G., Chadra, T. D., Widagdo, D., & Priatna, N. (2014). Pendidikan Matematika I. Tangerang Selatan: Universitas Terbuka.
Miyanto & Rifai, R. A. (2023). Matematika untuk SD/MI. Klaten: Intan Pariwara.